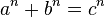ejemplos de tríos pitagoricos

>>> pitagoricos(18)
[(3, 4, 5), (4, 3, 5), (5, 12, 13), (6, 8, 10), (8, 6, 10), (8, 15, 17), (9, 12, 15), (12, 5, 13), (12, 9, 15), (15, 8, 17)]

Tríos pitagóricos

Un trío pitagórico se define como un conjunto de tres números, a, b y c que cumplen con la relación.

a2+b2=c2

Desarrolle un programa que contenga la función son_pitagoricos(a, b, c) que retorne True si a,b y c son un trío pitagórico, y False si no lo son:

>>> son_pitagoricos(3, 4, 5)
True
>>> son_pitagoricos(4, 6, 9)
False
>>> son_pitagoricos(5, 12, 13)
True

biografía de Fermat

Pierre de Fermat (Beaumont-de-Lomagne, Francia, 17 de agosto de 1601;¹ Castres,Francia, 12 de enero de 1665) fue un jurista y matemático francés apodado por Eric Temple Bell con el sobrenombre de «príncipe de los aficionados».²

Fermat fue junto con René Descartes uno de los principales matemáticos de la primera mitad del siglo XVII.

Descubrió el cálculo diferencial antes que Newton y Leibniz, fue cofundador de la teoría de probabilidades junto a Blaise Pascal e independientemente de Descartes, descubrió el principio fundamental de la geometría analítica. Sin embargo, es más conocido por sus aportaciones a la teoría de números en especial por el conocido como último teorema de Fermat, que preocupó a los matemáticos durante aproximadamente 350 años, hasta que fue demostrado en 1995 por Andrew Wiles ayudado por Richard Taylor.

Fermat es uno de los pocos matemáticos que cuentan con un asteroide con su nombre,(12007) Fermat. También se le ha dado la denominación de Fermat a un cráter lunar de 39 km de diámetro.

Fermat y wiles (demostracion)

En teoría de números, el último teorema de Fermat, o teorema de Fermat-Wiles, es uno de los teoremas más famosos en la historia de la matemática. Utilizando la notación moderna, se puede enunciar de la siguiente manera:

Si n es un número entero mayor que 2, entonces no existen números enteros a, b y c, tales que se cumpla la igualdad (con a,b,c no nulos): Pierre de Fermat

El teorema fue conjeturado por Pierre de Fermat en 1637, pero no fue demostrado hasta 1995 porAndrew Wiles ayudado por Richard Taylor. La búsqueda de una demostración estimuló el desarrollo de la teoría algebraica de números en el siglo XIX y la demostración del teorema de la modularidad en el siglo XX.